Light pollution depends on the light source CCT (MAGAZINE)

IAN ASHDOWN explains that artificial sky glow due to roadway and area lighting depends on the correlated color temperature (CCT) of the light sources. Choosing the best CCT involves tradeoffs between light pollution, visual performance, personal preferences, ecological concerns, and economics.

One of the unavoidable consequences of roadway and area lighting is light pollution. Light emitted from the luminaires and reflected from the ground is scattered by air molecules and aerosols, some of which is seen by observers on the ground as a diffuse glow that obscures the stars in the night sky. Still, roadway lighting is a safety requirement, yet selection of a warm CCT can minimize the impact on the dark sky. Unfortunately, CCT choice is not simple, and we will present the facts as to how CCT relates to light pollution, the performance of our outdoor lighting, and other factors.

Interested in more articles & announcements on applications in sciences?

Light pollution is often considered to be of concern mostly to professional and amateur astronomers, but it has wider-reaching effects than this. It disrupts nocturnal animal behavior, including mammals, birds, amphibians, fish, and insects. It also disrupts the circadian rhythms of humans, animals, and plants; and it has even been implicated in the global obesity epidemic - light pollution may be making us fat.

It has often been stated that cool white light sources result in greater light pollution because blue light is preferentially scattered by air molecules. Warm white light sources are preferred, it is argued, because less blue light means less sky glow. The International Dark-Sky Association's Fixture Seal of Approval program, for example, recently reduced the maximum allowable CCT from 4100K (neutral white) to 3000K (warm white).

Another justification for low-CCT outdoor lighting is that many people prefer it, especially in residential areas. The city of Davis, CA, for example, was obliged to replace newly-installed 4800K street lighting with 2700K luminaires at a cost of $350,000 following residents' complaints about "prison-white" lighting.

For and against warm CCT

Still, however, there are valid arguments against low-CCT lighting. The IES Lighting Handbook, Tenth Edition, for example, discusses the application of parking and area lighting with high scotopic-to-photopic (S/P) ratios to take advantage of mesopic vision and reduce photopic light levels (Section 4.12.3, Spectral Effects). Unfortunately, the S/P ratios for LED modules are dependent on their CCTs (Table 1).

Simply put, low-CCT lighting mostly eliminates the possibility of reducing minimum illuminances under mesopic viewing conditions. With higher-CCT lighting, you can lower the light level, thereby reducing energy usage and light pollution while maintaining safe visibility levels.

TABLE 1. Scotopic/photopic (S/P) ratio versus CCT for LED modules.

Another argument is that low-CCT LEDs are inherently less efficacious than high-CCT LEDs, due to both Stokes shift losses and the broadband emission of red phosphors that extend into the near-infrared. This translates, of course, into higher capital, operating, and maintenance costs for municipal and state agencies, with more luminaires or higher-wattage LED modules.

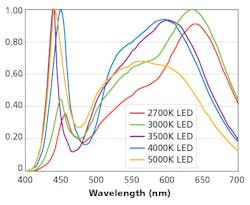
FIG. 1. Typical LED spectral power distributions normalized for maximum luminous intensity to be unity.

Finally, there is the problem of supply versus demand. Not all roadway and area luminaire manufacturers have offered low-CCT LED module options, or may do so at additional cost. That situation is changing, however, as LED makers deliver more-efficient and cost-effective warm-white LEDs.

What is the evidence?

The problem for professional lighting designers is that they may need to justify their design decisions and product specifications to the client. Given that the IDA Fixture Seal of Approval program is voluntary rather than mandatory for most jurisdictions, something more than a feel-good argument is needed. Lighting designers need quantitative facts.

FIG. 2. Photopic luminous efficiency function V(λ).

FIG. 3. Typical LED spectral power distributions normalized for constant luminous intensity.

Somewhat surprisingly, such facts are hard to come by. Light pollution has been of considerable concern to professional astronomers for the past half-century or so. There have been many academic papers published on the topic, with numerous mathematical models developed to model artificial sky glow. The topic of light source CCT has been of growing concern lately, especially with the recent focus on streetlight replacement with LED luminaires and a move to cooler CCTs.

TABLE 2. Scattering exponent versus distance from city center.

Unfortunately, the astronomical research community is not talking to the roadway and area lighting community. Seriously, how many lighting professionals read the Monthly Notices of the Royal Astronomical Society or the Journal of Quantitative Spectroscopy & Radiative Transfer? Conversely, how many professional astronomers read LEDs Magazine?

Fortunately, we can short-circuit this failure to communicate by borrowing the results from the latest of these aforementioned mathematical models and performing some simple and straightforward spreadsheet calculations. The outcome is what we need - quantitative facts concerning the relationship between light source CCT and artificial sky glow.

From apples to supercomputers

The first computer program that modelled artificial sky glow due to roadway lighting was developed in 1986 by the astrophysicist Roy Garstang, who executed his program on an Apple II computer. Thirty years later, Garstang's mathematical model of atmospheric optics is still considered valid and is being used in current research.

There is also, however, a program called Illumina, developed by University of Sherbrooke physicist Martin Aubé. This program implements a much more comprehensive, voxel-based radiative flux transfer algorithm that can require weeks of computer time on a supercomputer with several thousand CPUs and terabytes of RAM.

The situation is similar to weather prediction models, where a simple model such as Garstang's will give you a rough idea of what is going to happen, but it requires a supercomputer to perform massive amounts of data processing in order to have full confidence in the predictions. Simply put, Illumina models light pollution in a manner that would have been inconceivable thirty years ago.

For our purposes, the results are amusingly similar to the supercomputer Deep Thought in Douglas Adam's comic sci-fi novel The Hitchhiker's Guide to the Galaxy. It took Deep Thought 7.5 million years to determine that the answer to the "Ultimate Question of Life, the Universe, and Everything" was ... 42. In our case, the answer varies between 2.7 and 3.6.

Rayleigh and Mie scattering

Understanding the mathematics of sky-glow prediction models requires a good understanding of atmospheric optics. As an indication of the complexity, Garstang's equation for sky brightness, measured in nanolamberts, looks like this:

But we don't need to fully comprehend the complexity of the equation if we are only interested in the relationship between CCT and sky glow.

Light pollution is due to both Rayleigh scattering from air molecules and Mie scattering from aerosols such as dust, smoke, and haze. Rayleigh scattering is strongly wavelength-dependent, with a probability proportional to λ^-4, where λ is the wavelength. The sky is blue because of Rayleigh scattering. Mie scattering is wavelength-independent, which is why the clear sky appears pale blue or white in heavily-polluted urban areas.

What Aubé found with Illumina is that the combination of Rayleigh and Mie scattering results in a wavelength dependency described by λ^-α, where α varies from 3.6 to 2.7 as the distance from the city center increases. Table 2 neatly summarizes the 2.7 to 3.6 range for α that we hinted at earlier.

Now let's apply Aubé's results to the question of the influence of CCT on sky glow. First, we need some representative white-light LED spectral power distribution (SPD) data. Consider Fig. 1. The SPD curves were digitized from Lumileds' Luxeon Rebel product catalog with the SPDs normalized so that the largest value is unity.

To provide a fair comparison, these SPDs need to be scaled such that the LEDs generate the same luminous intensity. To do this, we multiply the SPDs by the photopic luminous efficiency function represented by the graph in Fig. 2 at 5-nm intervals. We then sum the results to obtain the relative photopic luminous intensities and normalize the sums to unity at the 3000K CCT (Table 3).

Calculating sky glow

Next, we will perform some math that will move us closer to determining the sky glow associated with LEDs across the CCT range. We divide the original normalized LEDs' SPDs by the values in Table 3 to produce the new SPDs in Fig. 3 that are now normalized for constant luminous intensity. The figure shows the different absolute SPDs of the street lighting located at a theoretical city center for each CCT, assuming the same luminous flux output.

Now, using Aubé's results and assuming an observing site 80 km (50 miles) from the city center, we multiply each 5-nm interval by (λ/550 nm)^-2.7 to represent the wavelength dependency, yielding the SPDs of the sky glow at 50 miles (Fig. 4).

FIG. 4. Overhead sky glow spectral power distribution at 50 miles.

This figure reveals precisely what we might expect - blue light is preferentially scattered, bolstering our assumption that high-CCT lighting results in increased sky glow. These SPDs represent the relative spectral radiance distribution at zenith from the observing site, which is perhaps the most useful definition of sky glow. If we assume scotopic (i.e., dark-adapted) visual observing conditions, we need to multiply these SPDs by the scotopic luminous efficiency function (Fig. 5) at 5-nm intervals to derive data typical of the nighttime setting.

TABLE 3. Relative photopic luminous intensity versus CCT normalized to 3000K.

We again must sum the results to obtain the relative scotopic zenith luminance. The results are shown in Table 4 normalized to 3000K. Indeed, this table contains the quantitative facts that we need.

Astronomical considerations

According to Table 4, the increase in scotopic sky brightness for 4000K LEDs compared to 3000K LEDs is only 12% percent. Our perception of brightness, following Steven's Power Law for extended light sources, means that we would see an increase in perceived sky brightness of only 4%! Surely this is not a reasonable justification for the IDA reducing the maximum allowable CCT from 4100K to 3000K for its Fixture Seal of Approval program?

Professional and amateur astrophotographers would vehemently disagree. Richard Wainscoat, principal investigator of the NASA-funded Pan-STARRS search for Near Earth Objects at the University of Hawaii, aptly called spectral power distributions of high-CCT LEDs such as that shown in Fig. 4 as the "nightmare spectrum." The power at 440 nm of a 5000K LED is about triple the power of a 3000K LED.

TABLE 4. Relative sky glow luminance at 50 miles from city center.

Unfortunately, the peak emission around the 450-nm range is right in the spectral region where natural airglow is low and there are important astronomical element absorption and emission lines. Astronomers use the measured intensities of these spectral features to determine the relative abundance of hydrogen, helium, and other elements in stellar atmospheres and nebulae. Unlike the basically monochromatic emissions of low-pressure sodium lamps, it is impossible to effectively filter out the blue LED emissions with band rejection filters. Limiting the CCT to 3000K reduces the contribution to light pollution in the blue region of the spectrum by a factor of two to three.

Allowing 4100K LEDs may be acceptable for casual stargazing, but not for astronomical research or astrophotography.

Ecological considerations

If astronomers are concerned about light pollution, ecologists and biologists have even more reason to be concerned. Light pollution impacts animals by disrupting orientation during migration, modifying breeding behavior, and changing predator-prey balances.

Of particular concern is that animals see the world differently from humans and respond accordingly. Wild mice, for example, have retinal cones whose responses peak at 370 nm (ultraviolet) and 530 nm (green). Sea turtle hatchlings are attracted to blue but not yellow light. Conversely, some nesting birds are adversely affected by white or red light but not green. Bats and many flying insects are sensitive to ultraviolet radiation but not red light. Changes in the nighttime behavior of flying insects will impact both bats and many amphibians.

FIG. 5. Scotopic luminous efficiency function V'(λ).

The effects of light pollution on ecological systems are complex and the subject of ongoing research. From the lighting designer's perspective, it is necessary to be at least cognizant of these issues, particularly where outdoor lighting will be located near wetlands or wildlife preserves.

Summary

Choosing the appropriate CCT for a roadway or area lighting installation is not an easy task. From a dark-sky perspective, it probably does not matter whether 3000K or 4100K LED modules are specified. For astronomical observations, however, 3000K is a better choice.

This choice, however, must be balanced against the possibility of reducing minimum illuminance levels with mesopic multipliers; the preferences of homeowners on residential streets; the capital, operating, and maintenance costs of less-efficacious low-CCT LED modules; and possibly site-specific ecological considerations.

Choosing the appropriate CCT is not an easy task, but it is at least made somewhat easier with quantitative facts.

IAN ASHDOWN, FIES, is a senior scientist at Lighting Analysts Inc. (agi32.com).